Heads I Win

A few months back I had a big battle with one of my oldest, most sensible friends.  We, along with another sharp buddy, went to graduate school together.  Along with an MIT guy (smarter than all three of us) we all started working at the same firm in 1999, me in our London office, and the others in Boston.  All but one have since changed firms, but we’ve done a pretty good job staying in touch.

Periodically, we all try to meet somewhere that isn’t London or Boston, and spend a few days talking about all sorts of stuff.   A little about life and a lot about companies, markets, and the business.  We always have a great time.  Although on this last trip, I’m not sure the others enjoyed it as much as they usually do.  Because, as I said my buddy and I were battling.  

We battled at breakfast, during the day, at dinner, and into the night.  

What were we battling about?

Coin flipping.  

Not really coin flipping, but essentially coin flipping.  

As we sat at the dinner table our first night there, there was a couple sitting next to us.  They could have been married, or just friends.  I don’t know.  But I asked my buddy this question.

“Imagine that I told you that that couple has two children, and that one of them is a girl.  What are the odds that their other child is also a girl?”

He asked if this was a trick question.  I said “nope.”  I then stated there were no funnies here; the outcomes were random, they were one or the other, and either were equally likely.  He said “50%”, or 1/2.  I responded that he was wrong.

And for the next three days, all we did was argue about it.

The answer is 1/3.

And that’s the end of this blog post.

Just kidding.

This is an old paradox in mathematics and statistics, and unless you are Thomas Bayes, it’s a tough one to visualize.  If we get back to the dinner table, it all becomes a little easier if we imagine that both of the couple’s children are outside playing together, along with three other sets of siblings. And that each of the four sets of children represents the way that a couple can have two kids.  And to be clear, here are the four ways.

‍

‍

That’s it.  Those are the four ways to have two kids, and as mentioned above, each is equally likely. There is a 25% chance of having two kids the first way, 25% the second way, and so on.

But when one girl emerges from the playground and sits with her parents at the dinner table, something interesting happens.  The initial odds that she has a sister didn’t change.

What did change is that we have eliminated “the fourth way”.  With the girl sitting down at the dinner table, we now know they didn’t have two boys.  So the sample space now looks like this:

‍

‍

Now, we don’t know which “way” the girl came from, but it could only be the 1st, 2nd, or 3rd way.  And this is where it gets interesting.  Since we now see the girl, we know she either has a big brother (the 1st way), a little brother (the 2nd way), a big sister (in the 3rd way), or a little sister (also in the 3rd way).

We can then shade out those possibilities for one child, and see what remains for the other child.  The nuance here is that in the “third way” the first girl can either be one child or the other child.

‍

‍

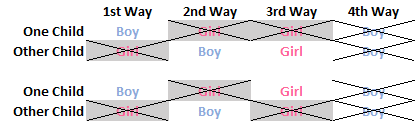
And whether she is one or the other, any way you slice it, two boys and one girl remain in each sample set.  So the odds of the girl having a sister, aka the odds that the two-child couple with one daughter having another daughter, are one-in-three.

Counterintuitive, right?  My buddy sure thought it was.[1]  

In Do Dice Play God?, Ian Stewart writes about this paradox.[2]  In it he shows that the extra information (that one child is not a boy) rules out “Boy, Boy” but it doesn’t change the initial probabilities.  Leonard Mlodinow highlights the same brain teaser in The Drunkard’s Walk.[3]  In fact, this boy-girl paradox has similarities to the well-documented Monty Hall problem.[4]  In that better-known paradox, Monty Hall cuts the sample space down, eliminating one possibility – but his action didn’t change the initial (lower) probability that the contestant picked a new car with his first choice.

And in this boy-girl paradox, the new information about there being at least one girl metaphorically means one of the doors has been removed.  We are left with three cases, all equally likely.  “Boy, Boy” is now irrelevant because it can’t occur.  So there has to be a one in three chance of “Girl, Girl.”

I think my buddy is probably assuming that the girl he sees sitting down with her parents is the oldest girl.  In which case, yes, the odds are 50/50:

‍

‍

I posed this to him though, and he disagrees.  He just thinks I am crazy.

I even tried nerding out and using Bayes’ theorem.  Before knowing anything about the family, other than they have two kids, we both agreed there were four possible sequence of events in the sample space, GG, GB, BG, and BB.  Each with a probability of 1/4.  

So, using Bayes, if we let “E” be ”two girls” (GG) and F be “not two boys” then once we are told that the couple has at least one girl, the answer becomes conditional.  Thus, the probability of E given F (that is the probability of ”two girls” given “not two boys“) is:

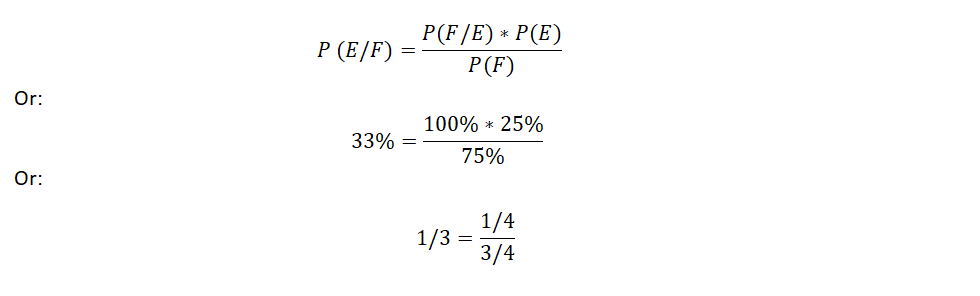
But my buddy still wasn’t buying it.  In his precise words:

“In the process you have convinced yourself that knowing the outcome of one independent variable, somehow influences the odds of a second independent variable.  I honestly have no idea how to logically convince you that can’t be right, other than to point out it should be obvious, given the definition of what an independent variable is.  To be clear, I am 100%, absolutely, and without reservation, convicted in my point of view on this and in my math on everything I’ve said.”

The good news is, we’re still friends.  As Ron Burgandy[5] (for whom we both have deep mutual respect) might say, we’ve “agreed to disagree.”

There is one other way to see it, and that is to use coins, and start flipping them two at a time.  It’s basically the same problem if I ask “if I flip two coins, and at least one of them is tails, what are the odds that the other one is also tails?”  

‍

So grab your daughter, ask her to close her eyes, flip two quarters, and then cover them.  Peek at them yourself, and if they are both heads, play again.  But if one of them is tails, show it to her, and ask her if she wants to bet on the other coin being tails.  You’ll give her a quarter if it is tails, and she’ll give you a quarter if it is heads.

She’ll probably think it is 50/50, so a fair bet.  But it isn’t.  There’s just a 33% chance of that the other coin is also tails.  You’ll take all her money, and teach her a subtle lesson about conditional probabilities.

Party tricks, deteriorating friendships, and poor parenting aside, this whole episode illustrates just how difficult it is to “think Bayesian”.  It is unnatural.  So unnatural that when every bone in our body is telling us 50%, it isn’t, even when presented with the facts.  

So how are we supposed to predict where the market is going to go?