Woody was Right

If you are managing a portfolio of equity investments, whether personally or institutionally, there are many factors that (should) go into its construction.  

For those that think yesterday’s risk metrics matter tomorrow (we don’t) there are risk and volatility targets.  For mean-variance Markowitz types, there is the efficient frontier.  For those that care about benchmarks, that introduces a whole host of other things to worry about.  

But even for those that make just a few investments in (hopefully) great ideas, what should one do?  Should you just equal-weight them?  Maybe, but what if you like one idea more than the other?  What if the upside is greater for one than the other?  What if the downside is worse?  What if the upside and downside is the same for two separate ideas, but you think the probability of success is better for one than the other?

We believe those things matter.  We also believe that, with limited capital, your decision to allocate to one name is related to the opportunity cost of investing in something else.  From there, it actually is not that difficult to decide how much capital to allocate to which stocks you want to buy. In fact, this process may help you realize that there are stocks which you thought you liked, but you actually don’t want to buy.

Here are the questions we ask ourselves about each position (and spend the majority of our time attempting to determine).

1. Where will the stock go if we are right?
2. How bad will things get if we are wrong?
3. What is our conviction that we are right?
4. How long is it going to take Mr. Market to figure out we are right or wrong?

Some readers will have observed we essentially have stated some of the variables inside the Kelly Criterion.  Well, that’s exactly what we have done.  

There is more information in the footnotes below about Kelly, but essentially, we think this is the way to go in terms of optimally deciding how much of our capital should be invested in each potential portfolio security.

Back at Bell Labs in the 50s, Kelly was basically riffing off of Claude Shannon, who had been working on a formula that attempted to measure how much bandwidth was needed to transfer information.  The more unpredictable or unreliable the information was, the more bandwidth it required.  More importantly, the information could be bad, and that took up bandwidth, and affected the rate of good information being transmitted across the channel.  

Well, John Kelly worked at Bell Labs too, alongside Shannon.  Kelly realized that the “information rate” analysis was basically all about probabilities and payoffs, and thus had applications beyond that of making phone calls across the Atlantic Ocean.  In other words, he thought “hey, this might work for gambling too.”

Thus the Kelly Criterion was born.  Shannon liked it so much that he and Ed Thorp took it to Vegas.

There are plenty of places where you can do a deep dive to learn more about the math behind Kelly, its proofs, and why geometric means dominate arithmetic means, but the bottom line is that smarter guys than all of us use it, and none of us that didn’t study under Paul Samuelson or Eugene Fama need to overcomplicate it.

Here are the variables:

And this is the equation:

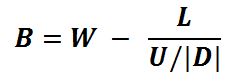
That’s it.  That’s Kelly.

Now investing is not gambling.  It is much more unpredictable.

In investing, we don’t know the payoff, we don’t know the downside, we don’t know the probabilities, and we don’t know how long the game is going to take.  But we can estimate them, and if we are good at estimating them ex-ante, then perhaps the Kelly Formula can help us to size our investments too (and if we are better than our peers at estimating, we can generate alpha).

Here is an example, we’ll call it XYZ.

Stock XYZ trades for $12 per share, and we think that if everything goes as we expect, it will go to $18 per share (+50%).  We also think that if the risks we’ve identified bear out, the stock will drop to $9 (-25%) [2].  Moreover, we have 70% conviction in the upside case.  

So let’s fill it out:

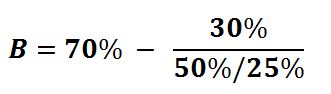
And after you solve for B, you see that the Kelly-recommended bet size is about 55% of your bankroll.  Now of course, that seems crazily steep, but if you think about it from the perspective of a single-game player that is going to parlay her bankroll into the next gamble, this actually is the way for her to geometrically maximize the outcome, without ever risking bankruptcy (as she can only ever bet a portion of her bankroll).  That said, one criticism from gamblers is that “full Kelly” is hard to swallow, and is difficult to stick with (due to behavioral biases like loss aversion).  Some folks will instead implement a “half-Kelly” strategy, or a “one-third Kelly” strategy, or whatever level they think they can implement objectively.

But the real-world nuance for us non-gamblers here is that portfolio managers and investors don’t just manage one single investment at a time.  At Albert Bridge, we manage a portfolio of 20 or so ideas, concurrently.  But don’t worry, there are plenty of easy fixes.  Our workaround is to determine the individual recommended Kelly bet size as if it were a single game, then aggregate all those figures, and then proportionally assign the capital to the security related to its relative suggested Kelly size. [3]  

It sounds complicated, but it isn’t.  

Imagine stock XYZ above with a suggested Kelly bet size of 55%.  Then imagine four other positions, with different Kelly-recommended bet sizes.  Then imagine we want to hold back 5% of our cash, and thus invest 95% of our bankroll (our portfolio) into these five ideas.  Here is what that would look like.

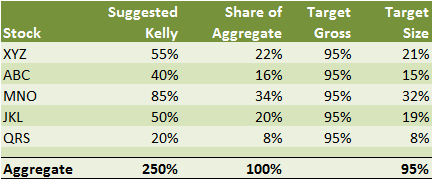
So, here XYZ would capture 21% of your bankroll, or your portfolio, not 55%.  With more investments, this figure would fall, but the amount of capital allocated to XYZ would always be related not just to its own expected returns, but those of all the other names in the portfolio.

We manage a portfolio that typically is 20-25 names, and this is basically how we decide to allocate the capital.  You can make it more complicated if you like.  In fact we do a little bit (see below) [4] but the bottom line is that using the framework for deciding how to allocate your capital helps to eliminate bias in your decision-making, and bet-sizing.[5]

And, sure, we can really screw things up.  We can be wrong about the downside.  We can under or overestimate how long it will take for us to discover that the upside or downside case played out.  And most importantly, especially because we all are overconfident, we can assign wrong (sometimes egregiously wrong) probabilities to the upside case.

So this is as much (in fact more) art as it is science.  So we should seek to minimize our own biases and enhance our objectivity, and then realize that the remaining art is going to be there whether you use Kelly or throw a finger in the air, so it’s probably best to use Kelly. [6],[7]