How Did This Even Happen?

No, I’m not talking about the winner of the Presidential election or COVID-19 or 2020.  I’m talking about something I saw Rex Chapman tweet out over the weekend.  This is not only incredible to watch, but even more fascinating to think about.  If it is real, it is statistically mind-boggling.

https://twitter.com/RexChapman/status/1322925488327843841

The quick synopsis of the video above is that a kid playing in a baseball game hits a random foul ball toward another player on an adjacent field who was also playing, but in a different baseball game.  The other player is actually up to bat, and in the batter’s box. Unbeknownst to him - and the pitcher throwing at him - the foul ball actually comes down into the strike zone at precisely the same time and same mid-air spot where the pitcher has pitched, and the batter connects on both balls in a single swing of the bat.

So, what in the world (or beyond) are the odds of this happening?  

So let’s start with a baseball diamond, and the likelihood that there is a game even happening.  Not an empty field, not a practice, a game.  During baseball season, a lot of baseball is played every week in America, but much of it is practice.  So, during a any given week, let’s say on average that there are three actual games played on a particular field.  If each game is about 100 minutes long, that is five “gamehours” during the week.  Furthermore, if we say that the “playable hours” are between 4:00 and 9:00 on weeknights, and 8:00 am to 9:00 pm on weekends, that is 51 hours a week that baseball could be happening.  So a field is being utilized for a game about 10% of the time it could be.  

In Rex’s video here though, there is this other game happening at the same time, on a field that is nearby enough that foul balls can reach into the field next door. This part of the analysis depends on the ratio of single diamond baseball facilities vs multi-field complexes.  Let’s say a quarter of all games at any given time have at least one other diamond next door, and that there is a 30% chance they are actually playing as well.  So now, if we randomly pick a baseball diamond across the country during baseball-playing hours, and go visit hoping for a game, we are down to a 0.7% chance (10%*25%*30%) that we will pick a venue where not just one but two baseball games are happening simultaneously.  

That’s just about 136-1 against.  So far, not crazy.

Now let’s go to that specific multi-field complex, where we learn upon arriving that there is not just one game happening, but two; and let’s turn on our camera and see if miracles happen.  To decompose the miracle in Rex’s video, let’s start with the kid that hit the foul ball in the first place.  Someone had the pitch the ball to him.  

In two-hour nine inning games, how many batters does a pitcher (or group of pitchers) face? How many pitches do they make to each batter?  How much time is there in between each pitch?  If a team sends up 35 batters in nine innings, and the other team does the same, and each batter sees an average of, say, four pitches, that is 280 pitches seen over 100 minutes of baseball.[i]  That is about 2.8 pitches every minute.  

Now, how many of those pitches are fouled off?  Let’s say 15%, so that works out to about two foul balls every five minutes (including the waiting time between batters and pitches), or 0.4 foul balls every minute.

The next question is about where that foul ball goes, and it isn’t as simple as about where the foul ball lands, but we will start there.  Rudimentary, I know, but let’s say there is 300 feet of foul territory down the left field line and beyond, and the same down the right, 200 feet left or right of home plate, and 100 feet behind it.  Let’s say the possible places for a foul ball to land looks something like the blue shading in the graphic to the right.  Using these numbers, there is nearly about 85,000 square feet of foul ball territory.

And since a standard baseball is about 2.9 inches in diameter, that means we can fit nearly 1.5 million balls on the ground of foul ball territory.  

Now, foul balls that are hit ten feet behind home plate, or indeed fouled into the backstop, are a lot more common than pop fouls that go over the backstop and fly into the field next door; but at this stage of the analysis, let’s assume they are all equally likely.  So, with this, given the likelihood of foul balls during a game are ~0.4 per minute (or 0.007 foul balls per second), then in any given second, the likelihood of a pitcher throwing a pitch that is fouled off in precisely one pre-determined place are about 208 million-to-1. If anything, since we are indeed talking about a pop foul that presumably went about 80-100 feet backwards, the odds are even longer.  A batter is probably (I’ll guess) three times more like to foul into the dirt, or tip foul, or foul into the backstop as he is to foul one deep behind him.  That takes us out to nearly 624 million-to-1 against.

But this isn’t even about where the foul ball lands.  The second batter isn’t golfing, he’s playing baseball.  So it is about where it is in the air before it lands, and perhaps it is about when it is in the air before it lands.  

As suggested above, the “where” of it is most likely straight into the dirt.  But we will consider that some fly balls go 80 feet into the air, this expands the “foul ball territory space” to the Z axis.  And if you can stack 332 baseballs 80 feet high, then we can figure out the volume here.  Basically, as we have defined it here, with our 85,000 square feet of foul ball territory going 80 feet high, we can fit over 480 million baseballs into the three-dimensional space that constrains foul ball territory.  Yes, some areas are more likely than others, but we’ve corrected a little bit for this already with the 3x odds multiplier used above.

So, how long is that average foul ball in the air?  Since most of them go straight into the dirt or off the catcher, the answer is probably a lot less than half a second.  In this case shown by Rex above, it was probably between two and three seconds.  But I am not sure this question is relevant for the exercise (nor do I want to attempt to relearn the math).  I think we can get there without this variable.  Where we are now is that a batter on another field has fouled off a pitch thrown at a specific second that is not only hittable, but precisely where a batter will be swinging at another pitch.  

But even before we introduce the new pitcher and batter, we now know the odds, at a venue where we randomly dropped in to hopefully watch a baseball game today, against a foul ball being hit precisely to the z-axis place it needs to be for there to be a chance at this miracle. They are about 566 billion-to-1:

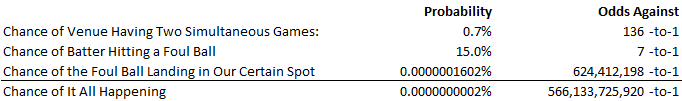
But hold on, we still need to introduce the second pitcher who is throwing 2.7 balls per minute, and he not only needs to throw the ball in the precise place as the arriving foul ball from the other field, but at the precise time.

Let’s say this second pitcher has good control, and he is almost throwing in the Ted Williams strike zone.  Baseball fans will be familiar with Ted’s wheelhouse, as pictured here.

Ted has 77 places where a hittable ball might come.  Yes, I know there are infinitely more, Xeno, but bear with me. Our second pitcher above needs to throw in the exact same spot where the foul ball is coming in from the other game, so if you are throwing hittable balls to Ted Williams, there is a 1-in-77 chance that this pitcher does just that.  But our pitcher might be not be major league caliber, nor might he even be trying to throw a strike.  He might be throwing one down and away. So, let’s say we are looking at a 1-in-125 chance in our case.

Then we are going to say that he makes 0.047 pitches per second, and this all works out to a likelihood that our second pitcher throws the ball at the right place, and at the right time, of just 0.037%, or 2,679-to-1 against.

And then the batter has to make contact!  In the bigs they do this about 75% of the time, so let’s say it is 60% here in Rex’s video.  That blows out our odds from 2,679-to-1 against to almost 4,500-to-1.

And now it gets even tougher, because seconds matter, and we are using seconds. Using “seconds” grossly underestimates the odds against this all happening.  It takes half a second (ish) for a pitched ball to reach home plate, but even dividing by two doesn’t solve this.  Think about it,  if the pitcher on the second field were to release his pitch just 0.1 seconds earlier or later, then his pitch just doesn’t arrive at the same time as the foul ball.  

But let’s go with tenths-of-seconds anyway (we should probably even go to hundredths). That means the odds of a batter making contact with a pitch thrown in the precise right spot with a one-tenth-of-a-second margin for error on when the ball arrives are about 45,000-1 against.  Actually, since the swing plane of the bat (the “bat-plane”) is probably four balls long, I will even divide that by four so that I don’t sound too much like Carl Sagan in my final conclusion below, so that gets us back to just over 11,000-to-1 against.  

And finally we can now calculate the joint-probability of this all happening.  Some might argue that this is a conditional probability, but for this exercise (at least) I am saying it all happens at the same time, and one is not conditional on the other.

The odds of a ball being thrown and then a foul ball being hit at the precise time which then crosses into the adjacent field’s batters box and landing in the precise spot as a pitch being thrown at just the right time and arriving at the same place, the batter connecting with both balls in a single swing, and that we just happen to be at the right place to see the event, are 6.3 quadrillion-to-one against.

That is one in 6.3 million billions.[i],[ii],[iii]

It will never, ever, ever happen again.